Generative vs discriminative
These two major model types, distinguish themselves by the approach they are taking to learn. Although these distinctions are not task-specific task, you will most often hear those in the context of classification.
Differences
In classification, the task is to identify the category $y$ of an observation, given its features $\mathbf{x}$: $y \vert \mathbf{x}$. There are 2 possible approaches:
-
Discriminative learn the decision boundaries between classes.
-
 Tell me in which class is this observation given past data.
Tell me in which class is this observation given past data. - Can be probabilistic or non-probabilistic models. If probabilistic, the prediction is $\hat{y}=arg\max_{y=1 \ldots C} \, p(y \vert \mathbf{x})$. If non probabilistic, the model "draws" a boundary between classes, if the point $\mathbf{x}$ is on one side of of the boundary then predict $y=1$ if it is on the other then $y=2$ (multiple boundaries for multiple class).
- Directly models what we care about: $y \vert \mathbf{x}$.
-
 As an example, for language classification, the discriminative model would learn to distinguish between languages from their sound but wouldn't understand anything.
As an example, for language classification, the discriminative model would learn to distinguish between languages from their sound but wouldn't understand anything.
-
-
Generative model the distribution of each classes.
-
 First "understand" the meaning of the data, then use your knowledge to classify.
First "understand" the meaning of the data, then use your knowledge to classify. - Model the joint distribution $p(y,\mathbf{x})$ (often using $p(y,\mathbf{x})=p(\mathbf{x} \vert y)p(y)$). Then find the desired conditional probability through Bayes theorem: $p(y \vert \mathbf{x})=\frac{p(y,\mathbf{x})}{p(\mathbf{x})}$. Finally, predict $\hat{y}=arg\max_{y=1 \ldots C} \, p(y \vert \mathbf{x})$ (same as discriminative).
- Generative models often use more assumptions to as t is a harder task.
-
 To continue with the previous example, the generative model would first learn how to speak the language and then classify from which language the words come from.
To continue with the previous example, the generative model would first learn how to speak the language and then classify from which language the words come from.
-
Pros / Cons
Some of advantages / disadvantages are equivalent with different wording. These are rule of thumbs !
-
Discriminative:
-
 Such models need less assumptions as they are tackling an easier problem.
Such models need less assumptions as they are tackling an easier problem. -
 Often less bias => better if more data.
Often less bias => better if more data.
- Often
 slower convergence rate . Logistic Regression requires $O(d)$ observations to converge to its asymptotic error.
slower convergence rate . Logistic Regression requires $O(d)$ observations to converge to its asymptotic error. -
 Prone to over-fitting when there's less data, as it doesn't make assumptions to constrain it from finding inexistent patterns.
Prone to over-fitting when there's less data, as it doesn't make assumptions to constrain it from finding inexistent patterns. - Often
 More variance.
More variance.
-
 Hard to update the model with new data (online learning).
Hard to update the model with new data (online learning). -
 Have to retrain model when adding new classes.
Have to retrain model when adding new classes.
-
 In practice needs additional regularization / kernel / penalty functions.
In practice needs additional regularization / kernel / penalty functions.
-
-
Generative
-
 Faster convergence rate => better if less data . Naive Bayes only requires $O(\log(d))$ observations to converge to its asymptotic rate.
Faster convergence rate => better if less data . Naive Bayes only requires $O(\log(d))$ observations to converge to its asymptotic rate. - Often
 less variance.
less variance.
-
 Can easily update the model with new data (online learning).
Can easily update the model with new data (online learning). -
 Can generate new data by looking at $p(\mathbf{x} \vert y)$.
Can generate new data by looking at $p(\mathbf{x} \vert y)$. -
 Can handle missing features .
Can handle missing features . -
 You don't need to retrain model when adding new classes as the parameters of classes are fitted independently.
You don't need to retrain model when adding new classes as the parameters of classes are fitted independently. -
 Easy to extend to the semi-supervised case.
Easy to extend to the semi-supervised case.
- Often
 more Biais.
more Biais.
-
 Uses computational power to compute something we didn't ask for.
Uses computational power to compute something we didn't ask for.
-
![]() Rule of thumb : If your need to train the best classifier on a large data set, use a discriminative model. If your task involves more constraints (online learning, semi supervised learning, small dataset, …) use a generative model.
Rule of thumb : If your need to train the best classifier on a large data set, use a discriminative model. If your task involves more constraints (online learning, semi supervised learning, small dataset, …) use a generative model.
Let's illustrate the advantages and disadvantage of both methods with an example . Suppose we are asked to construct a classifier for the "true distribution" below. There are two training sets: "small sample" and "large sample". Suppose that the generator assumes point are generated from a Gaussian.
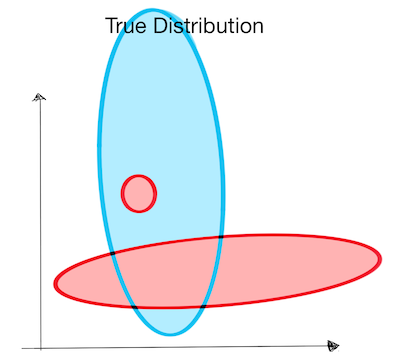
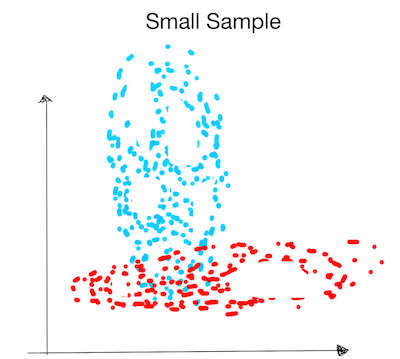
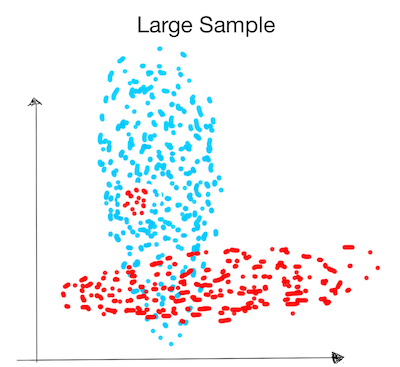
How well will the algorithms distinguish the classes in each case ?
-
Small Sample:
- The discriminative model never saw examples at the bottom of the blue ellipse. It will not find the correct decision boundary there.
- The generative model assumes that the data follows a normal distribution (ellipse). It will therefore infer the correct decision boundary without ever having seen data points there!
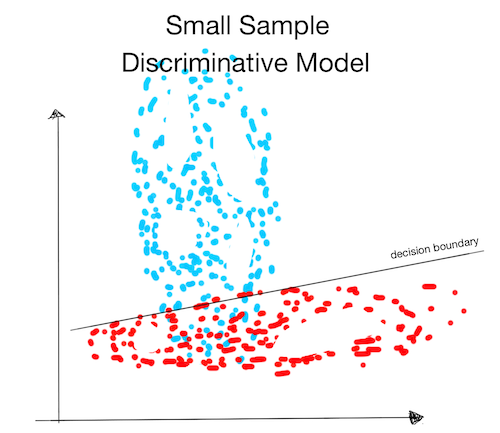
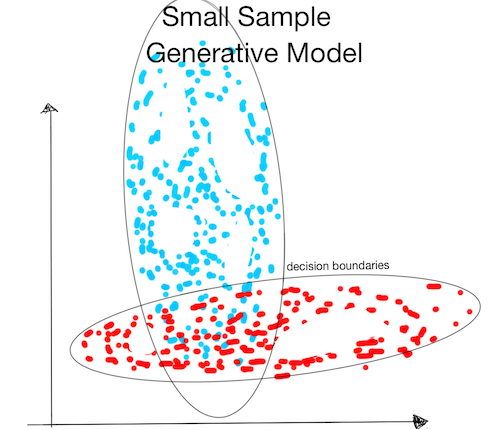
-
Large Sample:
- The discriminative model is not restricted by assumptions and can find small red cluster inside the blue one.
- The generative model assumes that the data follows a Gaussian distribution (ellipse) and won't be able to find the small red cluster.
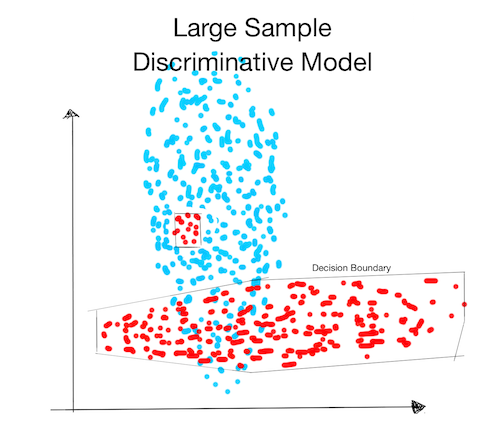
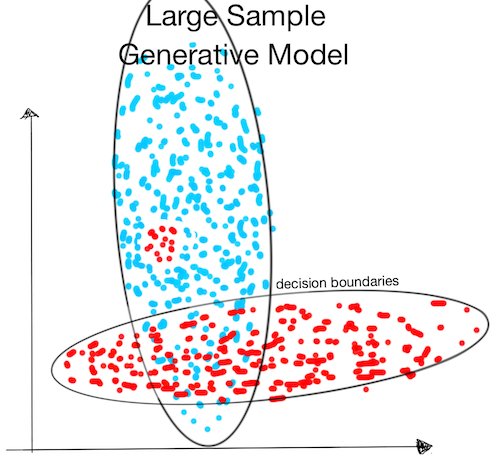
This was simply an example that hopefully illustrates the advantages and disadvantages of needing more assumptions. Depending on their assumptions, some generative models would find the small red cluster.
Examples of Algorithms
Discriminative
- Logistic Regression
- Softmax
- Traditional Neural Networks
- Conditional Random Fields
- Maximum Entropy Markov Model
- Decision Trees
Generative
- Naives Bayes
- Gaussian Discriminant Analysis
- Latent Dirichlet Allocation
- Restricted Boltzmann Machines
- Gaussian Mixture Models
- Hidden Markov Models
- Sigmoid Belief Networks
- Bayesian networks
- Markov random fields
Hybrid
- Generative Adversarial Networks
![]() Resources : A. Ng and M. Jordan have a must read paper on the subject, T. Mitchell summarizes very well these concepts in his slides, and section 8.6 of K. Murphy's book has a great overview of pros and cons, which strongly influenced the devoted section above.
Resources : A. Ng and M. Jordan have a must read paper on the subject, T. Mitchell summarizes very well these concepts in his slides, and section 8.6 of K. Murphy's book has a great overview of pros and cons, which strongly influenced the devoted section above.